NJU-Software Analysis-DataFlow Analysis Foundations

Iterative Algorithm, Another View

将每个节点的OUT视作一个集合，那么整个程序的空间可以表示为 (OUT[n1], OUT[n2], …, OUT[nk]), 可以视作空间$V^k$, 也就是每次迭代相当于一个函数F: $V^k$ → $V^k$, 将程序从一个状态点映射到另一个状态点。

算法的停止条件就可以表示为找到一个不动点，也就是F($V_i^k$) = $V_i^k$。

Questions:

1. 算法一定能停 or 一定能到达不动点吗?
2. 假设到达不动点，只有一个不动点吗？有多个的话，哪个是最好的 (most precise)?
3. 算法复杂度、最坏要迭代多少次？

Partial Order

对any $x\in P$:

a. 自反性: $x\le x$

b. 反对称: $x\le y,y\le x$, 则 $x=y$

c. 传递性: $x\le y,y\le z$, 则 $x\le z$

偏序关系中，集合任意两个元素不用必须可比，即可以不满足偏序关系。

Upper and Lower Bounds

S is a subset of P:

上界: $u\in P$ is an upper bound of S, if $\forall x\in S,x\le u$

下界: $l\in P$ is a lower bound of S, if $\forall x\in S,l\le x$

最小上界(lub or join 上确界): $\bigsqcup S$, for every upper bound of S, say u, $\bigsqcup S\le u$.

最大下界(glb or meet 下确界): $\sqcap S$, for every lower bound of S, say l, $l\le \sqcap S$.

$\bigsqcup S$ ⇐> $a\bigsqcup b$ (a join b)

$\sqcap S$ ⇐> $a\sqcap b$ (a meet b)

上/下界不一定有一个。最小上下界不一定存在，若存在则唯一。

Lattice, Semilattice, Complete and Product Lattice

Lattice: 给定偏序集($P,\le$)，对$\forall a,b\in P$, if $a\bigsqcup b$ and $a\sqcap b$ 都存在，则($P,\le$)是一个lattice。任意两个元素都有最小上界和最大下界。

Semilattice: 如果只有$a\bigsqcup b$存在，则称为join Semilattice; 只有$a\sqcap b$存在，则称为meet Semilattice。

Complete Lattice: 给点一个Lattice, 对任意一个子集S, 其最小上界和最大下界都存在，则这个Lattice称为Complete Lattice。

对于Complete Lattice, lub和glb都是最值: 有最大值 T(top) = $\bigsqcup P$, 最小值 $\perp$(bottom) = $\sqcap P$。

其实只要lattice有穷，那么就一定是complete lattice

但Complete Lattice不一定有穷

程序中一般是complete and finite lattice.

Product Lattice: 对n个lattice， 若都有lub和glb，则它们的笛卡尔积也是一个lattice。

DataFlow Analysis Framework via lattice

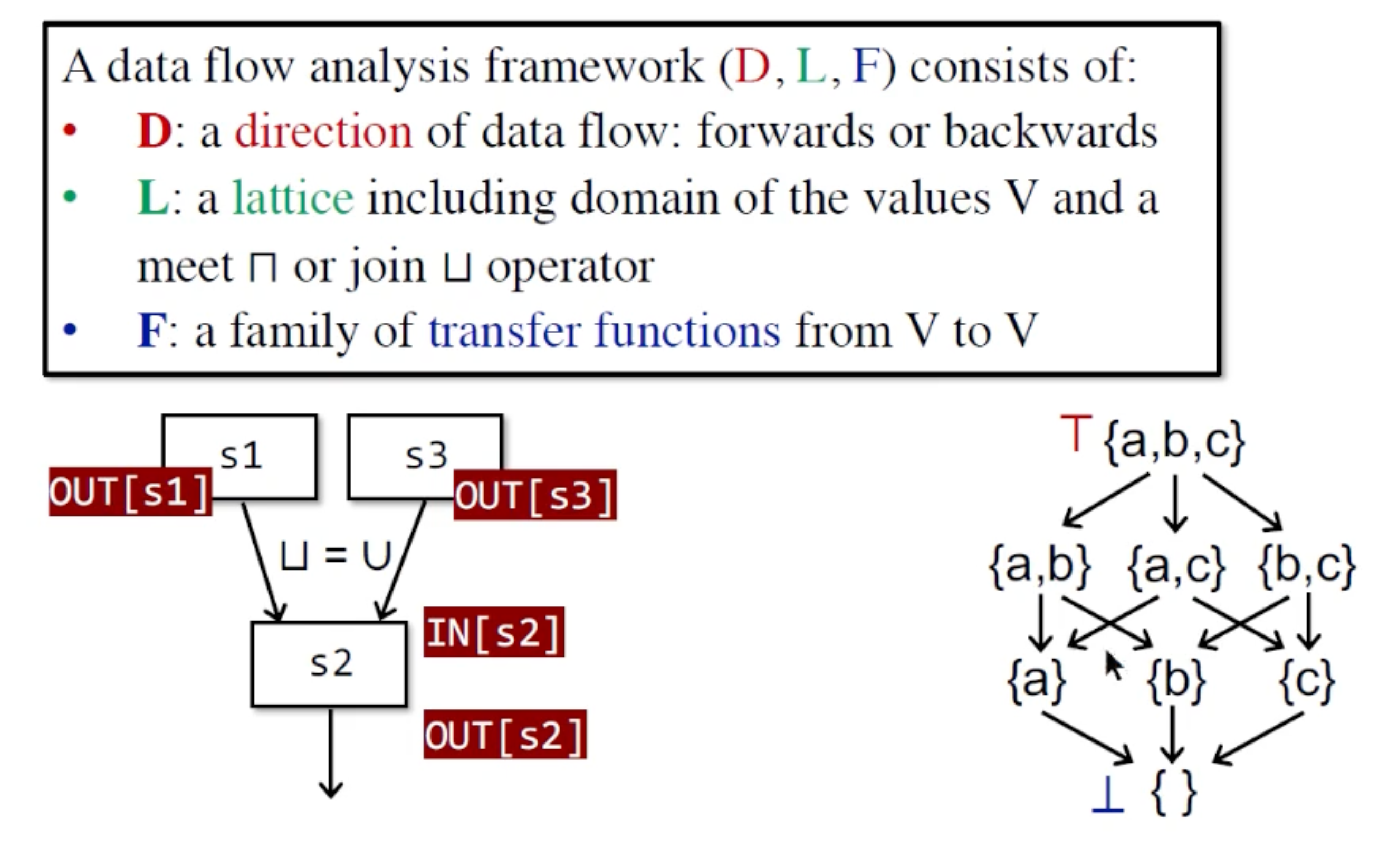
Review The Questions

1. 算法一定能停 or 一定能到达不动点吗?

2. 假设到达不动点，只有一个不动点吗？有多个的话，哪个是最好的 (most precise)?

About Lattice上函数的单调性 & 不动点定理

f:L → L (L is a lattice) is monotonic if $\forall x,y\in L$, $x\le y$ → $f(x)\le f(y)$

不动点定理: 若函数f单调，而且L是有限的，

1. 那么最小不动点可以通过迭代f($\perp$), f(f($\perp$)), …, $f^k(\perp )$ 得到。

2. 那么最大不动点可以通过迭代f(T), f(f(T)), …, $f^k(T)$ 得到。

Prove:不动点存在且是最小的那个

最小的证明就是数学归纳法就可以了:

1. f($\perp$) $\le$ f(x)

2. 假设 $f^i(\perp )\le f^i(x)$, 且f单调，那么 $f^{i+1}(\perp )\le f^{i+1}(x)$

3. 归纳到最后，$f^k(\perp )\le f^k(x)$

4. 因此$f^{Fix}$ = $f^k(\perp )\le x$

所以不动点是最小的, 而且求出的不动点也是唯一的

需要将数据流上的迭代算法映射到lattice上的函数，来将这二者建立联系。